Rexastor

Rexastor is being developed by Mikoláš Janota as a part of his PhD research. It is written in Java and will run correctly on any system with a 1.5/5.0 or later virtual machine.

Introduction

We present the tool on a small example. Formulas in Conjunctive normal form are formulas in Propositional logic, but the opposite does not hold. Therefore both share a common subset which could be reused in a type-safe way.

package pl; 
builtin String;
labels var, or, and, not, xor, imp;
alias Var -> var[String];

// General Proposition Logic ----

alias Pl.Or -> or[Pl.F, Pl.F];
alias Pl.And -> and[Pl.F,Pl.F]; 
alias Pl.Not -> not[Pl.F];
alias Pl.Xor -> xor[Pl.F,Pl.F];
alias Pl.Imp -> imp[Pl.F,Pl.F]; 

type Pl.F=Pl.Or | Pl.And | Pl.Not | Pl.Xor | Pl.Imp
    | Var ;

// CNF --------------------------

alias CNF.And -> and[CNF.F,CNF.F]; 
alias CNF.Or ->  or[CNF.Clause, CNF.Clause];
alias CNF.Not -> not[Var];

type CNF.F=CNF.Clause | CNF.And ;
type CNF.Clause = CNF.Lit | CNF.Or ;
type CNF.Lit = Var | CNF.Not ;

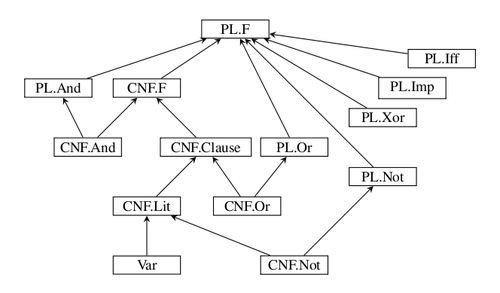
Relation definition First, we have to define the structure of CNF and Propositional logic (right). Rexastor automatically exploits the relation among components and builds type relation.

The subtyping relation on generated classes

Test example contains a small testing class which presents the functionality of the pretty printer.

import pl.Pl; // import Propositional logic
import pl.CNF; // import CNF logic

// statically import all constructs common to both logics
import static pl.Common.*; 

/** A tiny testing class for {@code PP} and subtyping on formulas.
 */
public class TestPP {
    public static void main(String[] args) {
        // Construction is done through static functions 
        // for conciseness reasons.

        // prepare a couple of variables
        Var a=Var("a");
        Var b=Var("b");
        Var c=Var("c");

        // construct two Propositional Logic formulas
        Pl.F f = Pl.Not(Pl.And(a, b));
        Pl.F f1 = Pl.Xor(a, c);

        // and one CNF formula
        CNF.F cnf = CNF.And(a, CNF.Not(b));

        // print via PP
        PP pp=new PP();
        System.out.println(pp.print(f));
        System.out.println(pp.print(f1));
        System.out.println(pp.print(cnf));

        // the following just shows that subtyping works as expected 
        Pl.F fFoo=cnf; // OK
        Pl.And fAnd=CNF.And(a, c); // OK
        CNF.F And1=CNF.And(a, c); // OK

        // uncommenting causes compilation error
        //        And1=fAnd;
        //        fAnd=And1;
        //        CNF.F cnfFoo=f1; // not OK
        //        CNF.F cnfBar=CNF.Or(CNF.And(a, b), c);
    }
}

Pretty printer

import static pl.Pl.*; // import all constructs for Propositional Logic
import static pl.Common.*; // import all constructs common for all Logics

/** A simple purely functional infix printer for Propositional Logic.
 */
public class PP extends MinVisitor<String> {
    private static String p(String s) { return "(" + s + ")"; }

    /** Converts a given formula to  a String representation. */
    public String print(F f) { return eval(f); }

    @Override public String visit(Var v, String s)  { return s; }

    @Override public String visit(Xor n, String first, String second) 
        {return p(first) + " XOR " + p(second);}
  
    @Override public String visit(Imp n, String first, String second) 
        {return p(first) + " => " + p(second);}
  
    @Override public String visit(Or n, String first, String second) 
        {return p(first) + " OR " + p(second);}
  
    @Override public String visit(Not n, String first) 
        {return "NOT" + p(first);}
  
    @Override public String visit(And n, String first, String second) 
        {return p(first) + " AND " + p(second);}

}

Visitor with memoization, partially generated by the tool

import static pl.Common.*;
import pl.Pl;
import pl.CNF;

import java.util.HashMap;

/** 
 * A visitor stub for depth-first search traversal. 
 */
public abstract class MinVisitor<R> implements Pl.FVisitor<R> {
    private final HashMap<Pl.F, R> m=new HashMap<Pl.F, R>();

    R eval(Pl.F n) { 
        // memoize
        R retv=m.get(n);
        if (retv!=null) return retv;
        retv=n.accept(this); 
        m.put(n, retv);
        return retv;
    }

  public final R visit(Var node) { return visit(node, node.getFirst()); }

  public final R visit(Pl.Xor node) {
    return visit(node, eval(node.getFirst()), eval(node.getSecond()));
  }

  public final R visit(CNF.Not node) {
    return visit(node, eval(node.getFirst()));
  }

  public final R visit(Pl.Imp node) {
    return visit(node, eval(node.getFirst()), eval(node.getSecond()));
  }

  public final R visit(CNF.Or node) {
    return visit(node, eval(node.getFirst()), eval(node.getSecond()));
  }

  public final R visit(Pl.Or node) {
    return visit(node, eval(node.getFirst()), eval(node.getSecond()));
  }

  public final R visit(Pl.Not node) {
    return visit(node, eval(node.getFirst()));
  }

  public final R visit(CNF.And node) {
    return visit(node, eval(node.getFirst()), eval(node.getSecond()));
  }

  public final R visit(Pl.And node) {
    return visit(node, eval(node.getFirst()), eval(node.getSecond()));
  }
 
  public abstract R visit(Var n, String first);
  public abstract R visit(Pl.Xor n, R first, R second);
  public abstract R visit(Pl.Imp n, R first, R second);
  public abstract R visit(Pl.Or n, R first, R second);
  public abstract R visit(Pl.And n, R first, R second);
  public abstract R visit(Pl.Not n, R first);

  // run parent visit methods   
  public R visit(CNF.Not n, R first) {return visit((Pl.Not)n);}
  public R visit(CNF.Or n, R first, R second) {return visit((Pl.Or)n);}
  public R visit(CNF.And n, R first, R second) {return visit((Pl.And)n);}
}